Functions on sets

For functions between domain X and codomain Y, which maps e.g. f(x)=y,

• Injection - is 1:1, so f(x)=f(w) implies x=w. However it isn't onto, so there may be some y∈Y for which there is no x such that y=f(x)
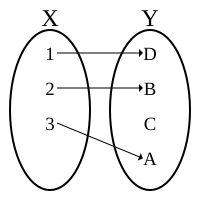
• Surjection - is onto, so the image of X is the whole of Y. For every y∈Y there is a x such that y=f(x)
  
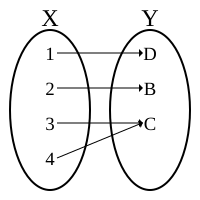
• Bijection - injection and surjection - one to one correspondence, with no unmapped members of either set.
  Bijections have an inverse which is also a bijection.

  Two finite sets between which there is a bijection have the same number of elements.

  If you can define a bijection between the set of positive integers and an infinite set S, then S is countable.

  The identity function on a set is a bijection.

function composition